I sistemi di numerazione¶
La scrittura in base 10¶
Il nostro sistema di numerazione è il sistema decimale. Ciò ha probabilmente origine dal fatto che abbiamo 10 dita. Forse se fossimo nati ragni avremmo contato fino ad otto ed useremo un sistema di numerazione ottale, se fossimo nati gatti avremmo contato fino a 4 e useremo un sistema quattrale, millepiedi fino a mille. Come conta un computer? Un computer capisce solo due stati: passa corrente o non passa corrente: è come se avesse due dita. Tutti i sistemi che oggi usiamo nell’informatica sono a due stati, si dicono ‘bistabili’: i circuiti elettrici possono trovarsi nello stato di acceso o di spento, i dischi magnetici dell’hard disk sono fatti di microscopici magneti che possono essere magnetizzati in un verso o nel verso opposto, i dischi ottici come i CD-ROM e i DVD si comportano come microscopici specchi che riflettono la luce oppure non la riflettono.
Nell’antichità si usava uno strumento chiamato abaco. Gli abachi erano tavolette suddivise in colonne su cui si spalmavano cera o sabbia e si incidevano segni o si mettevano sassolini.
Per contare un certo numero di oggetti e ricordarci quanti sono, utilizziamo un abaco:
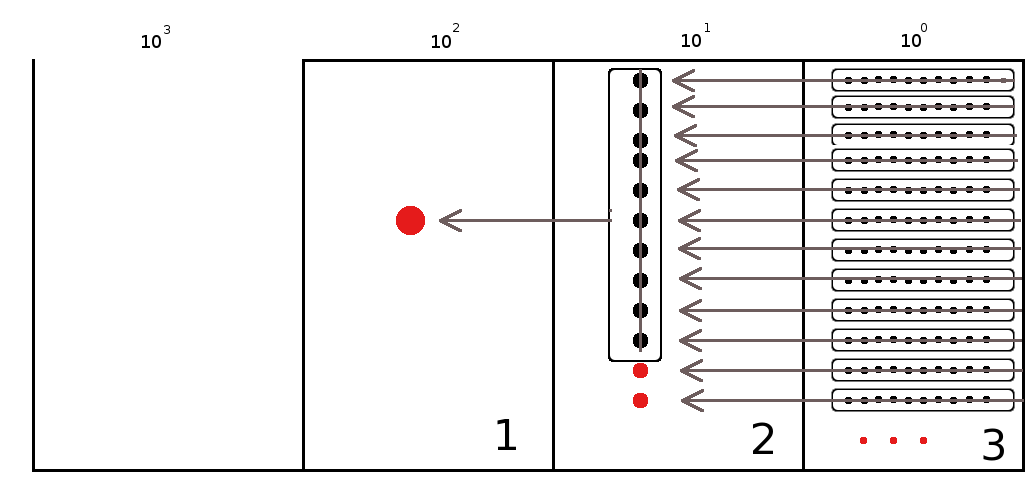
Cominciamo a contare con le mani: per ogni raggruppamento di 10 segniamo un’unità di ordine superiore, fino a contare tutti gli elementi del nostro insieme. Le unità che rimangono, perché non riescono a formare un raggruppamento di 10, vengono segnate con la cifra che le rappresenta: nel nostro caso 3.
Passiamo all’unità di ordine superiore: le decine. Anche con queste formiamo raggruppamenti di 10, se ci riusciamo. Ogni raggruppamento forma un’unità di ordine superiore. Se rimangono unità di questo ordine esse rappresentano decine. Se non rimane alcuna unità scriviamo 0. Nel nostro caso ne rimangono 2.
Il procedimento continua finché non abbiamo finito di contare tutti gli elementi. Nel nostro esempio finiamo dopo aver formato un’unità di ordine superiore. Il nostro numero è 123.
Naturalmente i due numeri 123 e 312 sono due numeri diversi anche se sono formati dalle stesse cifre: sono diversi perché la posizione delle cifre è diversa.
In generale, il valore dei numeri è diverso a seconda della posizione delle sue cifre. Il sistema di numerazione che solitamente usiamo è dunque un sistema posizionale: è chiamato decimale o a base dieci perché dieci unità di un determinato ordine formano un’unità di ordine superiore.
Riassumendo, abbiamo una serie di dieci simboli: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Il significato dei simboli dipende dalla posizione che assumono nella “parola” che rappresenta un numero.
Ad esempio: 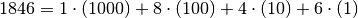
In particolare, scritto con le potenze del 10: 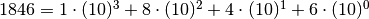
Se il numero è indicato come somma delle cifre per le potenze della base la scrittura si chiama notazione polinomiale.
Dieci è la base della rappresentazione, ovvero il numero di simboli usati, la potenza del 10 indica il peso (la posizione) che i simboli hanno nel numero.
Una volta compreso il meccanismo fondamentale su cui si basa il sistema di numerazione decimale, il procedimento si può estendere ad una base qualunque.
Se B è la base di un sistema, quando si formano B unità di un certo ordine, queste formano un’unità di ordine superiore. In questo modo si può costruire un sistema di numerazione con qualsiasi base maggiore di 1.
Scrittura di un numero in una base qualsiasi¶
Il procedimento usato per scrivere un numero in base 10 può essere usato per scrivere un numero in una base qualsiasi.
Esempio
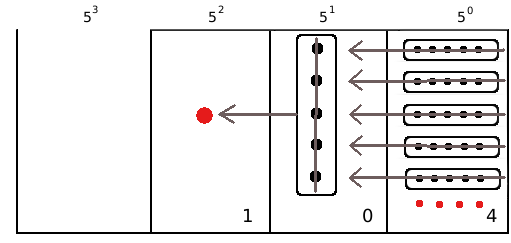
Contare 29 oggetti in base 5.
Come nel caso della numerazione in base 10, utilizziamo un abaco.
Invece di contare per dieci proviamo a contare per cinque. Invece di raggruppare per unità, decine, decine di decine e così via, conteremo raggruppando per unità, per cinquine, per cinquine di cinquine e così via.
Il numero che otteniamo si scrive 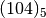 e si legge “uno-zero-quattro in base cinque” per distinguerlo da
centoquattro scritto in base 10.
e si legge “uno-zero-quattro in base cinque” per distinguerlo da
centoquattro scritto in base 10.
Per ottenere il numero decimale che corrisponde al numero scritto in base 5
occorre sviluppare il numero in base 5 nella sua scrittura polinomiale: 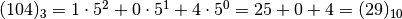
Esempio
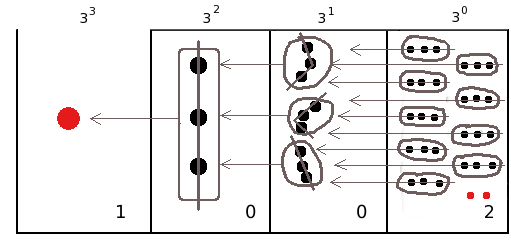
Contare 29 oggetti in base 3.
Questa volta dobbiamo contare per tre.
Il numero che otteniamo si scrive 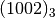 e si legge “uno-zero-zero-due in base tre” per distinguerlo da milledue
scritto in base 10.
e si legge “uno-zero-zero-due in base tre” per distinguerlo da milledue
scritto in base 10.
Per ottenere il numero decimale che corrisponde al numero scritto in base 3 occorre sviluppare il numero in base 3 nella sua scrittura polinomiale.
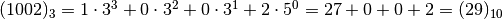
Riflettiamo su quanto abbiamo fatto negli esempi precedenti: i simboli che
occorrono per scrivere un numero in base 10 sono
dieci: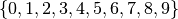 ; i simboli necessari per scrivere un numero in base 5 sono cinque:
; i simboli necessari per scrivere un numero in base 5 sono cinque:
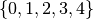 ; i simboli necessari per scrivere un numero in base 3 sono tre:
; i simboli necessari per scrivere un numero in base 3 sono tre: 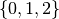 . Analogamente i simboli che serviranno per scrivere un numero in base 2 sono
due
. Analogamente i simboli che serviranno per scrivere un numero in base 2 sono
due 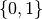 . Possiamo generalizzare e dire che i simboli necessari per scrivere un numero
in una base B qualsiasi sono B e precisamente
. Possiamo generalizzare e dire che i simboli necessari per scrivere un numero
in una base B qualsiasi sono B e precisamente 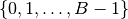
Possiamo scrivere i numeri anche in una base superiore a 10. Una base molto usata nell’informatica, insieme alla base 2, è la base esadecimale: cioè la base 16.
In questo caso, per contare devo fare raggruppamenti di 16. Sono necessari perciò 16 simboli per indicare questi raggruppamenti, pertanto occorrono simboli anche per i numeri 10 , 11, 12, 13, 14, 15...
I simboli convenzionalmente usati sono i seguenti:
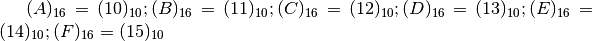
I numeri seguenti sono 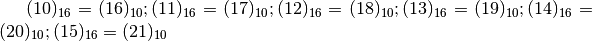
Convertire un numero da una base diversa da 10 a base 10
Per scrivere un numero da una base diversa da 10 a base 10 bisogna sviluppare il numero nella sua forma polinomiale.
Se 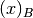 è un numero qualsiasi scritto nella base B e se
è un numero qualsiasi scritto nella base B e se 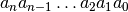 sono le cifre del numero
sono le cifre del numero 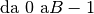
avremo:
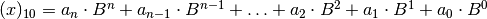
- Stabilire il valore di verità delle seguenti proposizioni:
- La scrittura 1234 può esprimere un numero in base 4 V/F
- Il valore numerico espresso in base 10 della cifra 2 nel numero (1523)6 è 72 V/F
- Il valore numerico espresso in base 10 della cifra 3 nel numero (321)4 è 12 V/F
- Il valore numerico espresso in base 10 del numero (321)4 è 57 V/F
- Scrivi il numero (3411)5 in forma polinomiale e trova il corrispondente numero decimale
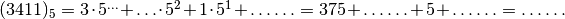
- Trasforma i seguenti numeri scritti in base diversa da 10 in un numero decimale
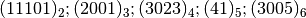
[29, 55, 203, 21, 653]
- Trasforma i seguenti numeri scritti in base 2 in un numero decimale
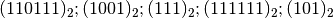
[55; 9; 7; 63; 5]
- Trasforma i seguenti numeri scritti in base 16 in un numero decimale
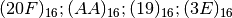
- [527; 170; 25; 62]
Convertire un numero da base 10 a una base diversa da 10
| Successive divisioni per 3 di 29 | Quozienti delle successive divisioni per 3 | Resti.. Warning, unrecognized: {urn:oasis:names:tc:opendocument:xmlns:text:1.0}line-breakdelle successive divisioni per 3 |
| 29 : 3 | 9 | 2.. Warning, unrecognized: {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line |
| 9 : 3 | 3 | 0 |
| 3 : 3 | 1 | 0 |
| 1 : 3 | 0 | 1 |
Abbiamo visto che per contare e scrivere un numero in una base diversa da dieci, per esempio 29 in base 3, dobbiamo raggruppare per 3. Raggruppare per 3 ha lo stesso significato che dividere per 3. Nella prima divisione per tre dei 29 oggetti il quoziente indica quante terzine otteniamo, mentre il resto indica quante unità di ordine 0 verranno considerate. Nel nostro esempio si ottengono nove terzine, mentre rimangono 2 unità di ordine 0. Il 2 sarà il primo numero a destra che verrà considerato. Con nove terzine si ottengono tre terzine di terzine con resto 0. Questo 0 diventa la cifra che scriviamo a sinistra del 2. Con tre terzine di terzine otteniamo una terzina di terzina di terzina, mentre rimangono 0 terzine di terzine. Questo 0 diventa il numero che scriviamo a sinistra dello zero precedente. Ora il quoziente di 1 diviso 3 dà come quoziente 0 con resto 1. Qui ci fermiamo e scriviamo 1 a sinistra dello 0 trovato precedentemente.
Il numero si scrive da destra verso sinistra prendendo i resti dal basso verso
l’alto, si ha 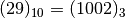 .
.
Controlliamo con la notazione polinomiale: 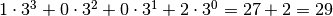 .
.
Esempio
Convertire nel sistema binario (in base 2) il numero 59.
Dividiamo successivamente 59 per 2 fino a che non otteniamo zero come quoziente e prendiamo come risultato della conversione la successione dei resti partendo dall’ultimo.
| Successive divisioni per 2 di 59 | Quozienti delle successive divisioni per 2 | Resti.. Warning, unrecognized: {urn:oasis:names:tc:opendocument:xmlns:text:1.0}line-breakdelle successive divisioni per 2 |
| 59 : 2 | 29 | {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line**1** |
| 29 : 2 | 14 | 1 |
| 14 : 2 | 7 | 0 |
| 7 : 2 | 3 | 1 |
| 3 :2 | 1 | 1 |
| 1 : 2 | 0 | 1 |
59 scritto in base 2 sarà 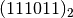
Verifichiamo con la scrittura polinomiale 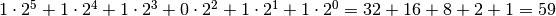
Esempi
Trasforma da base 10 a base diversa di 10
| b | a | s | e | 3 | b | a | s | e | 4 | b | a | s | e | 5 | |||||||||||||||||||
| 3 | 1 | 5 | 3 | 3 | 1 | 5 | 4 | 3 | 1 | 5 | 5 | ||||||||||||||||||||||
| 3 | 1 | 5 | 1 | 0 | 5 | 3 | 3 | 1 | 2 | 7 | 8 | 4 | 3 | 1 | 5 | 6 | 3 | 5 | |||||||||||||||
| {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line | 0 | 1 | 0 | 5 | 3 | 5 | 3 | 3 | 7 | 6 | 1 | 9 | 4 | 0 | 6 | 0 | 1 | {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line2 | 5 | ||||||||||||||
| 0 | 3 | 3 | 1 | 1 | 3 | 2 | 1 | 6 | {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line4 | 4 | 3 | 1 | 0 | 2 | |||||||||||||||||||
| 2 | 9 | 3 | 3 | 3 | 4 | 1 | 2 | ||||||||||||||||||||||||||
| 2 | 3 | 1 | 0 | ||||||||||||||||||||||||||||||
| 0 |
31510 = 1022003 31510 = 103234 31510 = 22305
Per trasformare i numeri da base 10 a base 2 basta scrivere il numero come somma delle potenze del 2:
- si parte dalla potenza del 2 più vicina, per difetto, al numero da convertire;
- si vede se la potenza precedente di ordine inferiore può fare parte della sequenza, cioè se la somma tra le potenze non diventa più grande del numero. Se può farne parte allora si scrive 1, altrimenti 0;
si prosegue in questo modo fino ad arrivare a 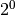 , cioè 1;
, cioè 1;
- la sequenza di 1 e 0, da sinistra verso destra, ottenuti è il numero binario corrispondente.
Esempio
Consideriamo ancora il numero 59.
Qual è la potenza del 2 più vicina, per difetto al 59? Il numero 32, cioè
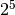 . Quindi
. Quindi 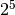
fa parte del numero binario. Scrivo 1 come primo numero della sequenza
Vediamo ora 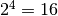 . Anche 16 può far parte del numero binario perché 32 + 16 = 48 che è
minore di 59. Segno 1 come secondo numero della sequenza
. Anche 16 può far parte del numero binario perché 32 + 16 = 48 che è
minore di 59. Segno 1 come secondo numero della sequenza
- Per lo stesso ragionamento anche
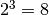
- fa parte del numero binario. Infatti 32 + 16 + 8 = 56, minore di 59. Segno
ancora 1 come terzo numero della sequenza.
- Invece
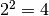
- non può farne parte perché 32 + 16 + 8 + 4 = 60, maggiore di 59. Segno 0
come quarto numero della sequenza.
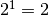
- e
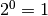 vanno bene e si arriva al totale voluto 59. Segno 1 come quinto e 1 come
vanno bene e si arriva al totale voluto 59. Segno 1 come quinto e 1 come
sesto numero della sequenza.
Riassumendo: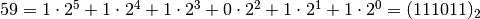
- Scrivere in base 2 i seguenti numeri in base dieci:
Risultati:math:[dots ; ( 100 )_{2} ; ...... ; ( 1100 )_{2} ; ......... ; ( 100001 )_{2} ]
- Scrivere in base 3 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( 2 )_{3} ; ( dots )_{3} ; ( 120 )_{3} ; ( ...... )_{3} ; ( 1000 )_{3} ; ( ......... )_{3} ]
- Scrivere in base 4 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( dots )_{4} ; ( 10 )_{4} ; ( 33 )_{4} ; ( ...... )_{4} ; ( ...... )_{4} ; ( 201 )_{4} ]
- Scrivere in base 5 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( 2 )_{5} ; ( dots )_{5} ; ( ...... )_{5} ; ( 22 )_{5} ; ( ......... )_{5} ; ( 113 )_{5} ]
- Scrivere in base 6 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:`[( dots )_{6} ; ( 4 )_{6} ; ( dots )_{6} ; ( 20 )_{6} ; (¶
)_{6} ; ( .... )_{6} ]`
- Scrivere in base 7 i seguenti numeri decimali:
Risultati:math:`[( 2 )_{7} ; ( dots )_{7} ; ( .... )_{7} ; ( .... )_{7} ; (¶
)_{7} ; ( 45 )_{7} ]`
- Scrivere in base 8 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( dots )_{8} ; ( dots )_{2} ; ( 17 )_{8} ; ( .... )_{8} ; ( 33 )_{8} ; ( ....... )_{8} ]
- Scrivere in base 9 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( dots )_{9} ; ( dots )_{9} ; ( 16 )_{9} ; ( ..... )_{9} ; ( ...... )_{9} ; ( 36 )_{9} ]
- Scrivere in base 16 i seguenti numeri:
| 2 | 4 | 15 | 12 | 27 | 33 |
Risultati:math:[( 2 )_{16} ; ( dots )_{16} ; ( F )_{16} ; ( dots )_{16} ; ( 1B )_{16} ; ( ...... )_{16} ]
Conversione di un numero da una base diversa da 10 a un’altra base diversa da 10
Esempio
Scrivere il numero 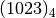 in base 7.
in base 7.
Per scrivere un numero da una base B a una base K tutte e due diverse da 10 occorre
- trasformare il numero in base B in un numero decimale attraverso la sua scrittura polinomiale;
- trasformare il numero decimale nella base K attraverso i resti delle divisione successive per K .
Applichiamo la procedura indicata:
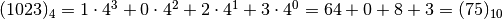
| Successive divisioni per 7 di 75 | Quozienti delle successive divisioni per 7 | Resti.. Warning, unrecognized: {urn:oasis:names:tc:opendocument:xmlns:text:1.0}line-breakdelle successive divisioni per 7 |
| 75 : 7 | 10 | 5.. Warning, unrecognized: {urn:oasis:names:tc:opendocument:xmlns:drawing:1.0}line |
| 10 : 7 | 1 | 3 |
| 1 : 7 | 0 | 1 |
Il numero scritto da destra verso sinistra con i resti delle successive
divisioni per 7 presi dal basso verso l’alto è 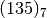 .
.
Le trasformazioni eseguite sono:
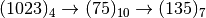
- Trasformare in base 7 i seguenti numeri scritti in base 4
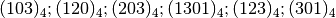
R::math:`[( 25 )_{7} ; ( .... )_{7} ; ( 50 )_{7} ; ( ...... )_{7} ; (
36 )_{7} ; ( ...... )_{7} ]`
- Trasformare in base 9 i seguenti numeri scritti in base 3
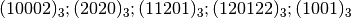
R::math:`[( 102 )_{9} ; ( dots )_{9} ; ( ...... )_{9} ; ( 518 )_{9} ;
( ...... )_{9} ]`
- Trasformare in base 16 i seguenti numeri scritti in base 4
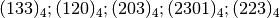
- R::math:`[( 1F )_{16} ; ( .... )_{16} ; ( 23 )_{16} ; ( .... )_{16} ;
( 2B )_{16} ]`
Conversione tra base 4, base 8, base 16 e base 2
Consideriamo il numero scritto in base 2 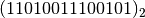 vogliamo scriverlo in base 4, in base 8, in base 16 senza passare dalla sua
scrittura in base 10. Infatti gruppi di due cifre in base 2 rappresentano tutte
le cifre della base 4, gruppi di 3 cifre in base 2 rappresentano tutte le cifre
della base 8, e gruppi di 4 cifre nella base 2 rappresentano tutte le cifre
della base 16, come indicato nella seguente tabella.
vogliamo scriverlo in base 4, in base 8, in base 16 senza passare dalla sua
scrittura in base 10. Infatti gruppi di due cifre in base 2 rappresentano tutte
le cifre della base 4, gruppi di 3 cifre in base 2 rappresentano tutte le cifre
della base 8, e gruppi di 4 cifre nella base 2 rappresentano tutte le cifre
della base 16, come indicato nella seguente tabella.
| Base 10 | base 2 | base 4 | base 8 | base 16 |
| 0 | 0 | 00 = 0 | 000 = 0 | 0000 = 0 |
| 1 | 1 | 01 = 1 | 001 = 1 | 0001 = 1 |
| 2 | 10 | 00.10 = 2 | 010 = 2 | |
| 3 | 11 | 00.11 = 3 | 011 = 3 | |
| 4 | 100 | 01.00 = 10 | 100 = 4 | |
| 5 | 101 | 01.01 = 11 | ||
| 6 | 110 | 01.10 = 12 | ||
| 7 | 111 | 01.11 = 13 | ||
| 8 | 1000 | 10.00 = 20 | 001.000 = 10 | |
| 9 | 1001 | |||
| 10 | 1010 | |||
| 11 | 1011 | |||
| 12 | 1100 | |||
| 13 | 1101 | |||
| 14 | 1110 | |||
| 15 | 1111 | |||
| 16 | 10000 | 0001.0000 = 10 | ||
| 17 | 10001 |
Da base 2 a base 4. Dobbiamo raggruppare il numero scritto in base 2 in gruppi di due cifre partendo da sinistra e tradurre con la corrispondente cifra in base 4.
| Numero scritto in base 2 | 1 1 | 0 1 | 0 0 | 1 1 | 1 0 | 0 1 | 0 1 |
| Numero scritto in base 4 | 3 | 1 | 0 | 3 | 2 | 1 | 1 |
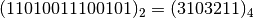
Convertire il numero da base 2 a base 8. Dobbiamo raggruppare il numero scritto in base 2 in gruppi di tre cifre partendo da sinistra e tradurre con la corrispondente cifra in base 8.
| Numero scritto in base 2 | 1 1 | 0 1 0 | 0 1 1 | 1 0 0 | 1 0 1 |
| Numero scritto in base 8 | 3 | 2 | 3 | 4 | 5 |
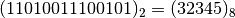
Convertire il numero da base 2 a base 16. Dobbiamo raggruppare il numero scritto in base 2 partendo da sinistra in gruppi di quattro cifre e tradurre con la corrispondente cifra in base 16.
| Numero scritto in base 2 | 1 1 | 0 1 0 0 | 1 1 1 0 | 0 1 0 1 |
| Numero scritto in base 16 | 3 | 4 | E | 5 |
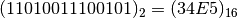
- Convertire in base 4, 8 e 16 i seguenti numeri scritti in base 2:
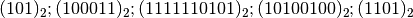
- Convertire in base 2 i seguenti numeri scritti in base 16:
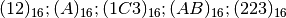
Perché è importante la base 2?
Tutti gli strumenti elettronici che utilizziamo hanno bisogno di tradurre le informazioni che inseriamo in stati fisici della macchina. Il metodo più semplice per tradurre in linguaggio macchina le nostre informazioni è utilizzare la base 2: composta solo dai simboli 0 e 1. La base 2 è quindi l’alfabeto a disposizione delle macchine per comprendere e rispondere alle nostre richieste. Se si utilizzasse la base 10 dovremo far riconoscere dall’apparato dieci differenti simboli che devono essere tradotti in dieci differenti stati.
A partire da questa informazione elementare detta bit (compressione dall’inglese di bi**nary digi**t) è possibile costruire informazioni più complesse sotto forma di sequenze finite di 0 e di 1. Attraverso la codifica binaria si è in grado di rappresentare caratteri, numeri, istruzioni di programma ma anche immagini, suoni e video.
Il primo multiplo del bit è il Byte che è formato da una sequenza di 8 bit:
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Con una sequenza di 8 bit possiamo codificare fino a 256 caratteri attraverso il codice ASCII. Quando digitiamo un carattere nella tastiera del PC mandiamo un impulso che è una sequenza di 8 bit. Vediamo alcuni esempi della codifica binaria dei caratteri
| Carattere | In base 2 | Numero decimale |
| A | 0 1 0 0 0 0 0 1 | 65 |
| a | 0 1 1 0 0 0 0 1 | 97 |
| M | 0 1 0 0 1 1 0 1 | 77 |
| m | 0 1 1 0 1 1 0 1 | 109 |
| 0 | 0 0 1 1 0 0 0 0 | 48 |
| 1 | 0 0 1 1 0 0 0 1 | 49 |
| à | 1 0 1 0 0 0 0 0 | 160 |
| ò | 1 0 1 0 0 0 1 0 | 162 |
Anche il byte ha i suoi multipli. Eccone alcuni indicati nella seguente tabella:
| Sistema internazionale | Utilizzo in informatica | ||||
| Nome | Marca | Potenze del 10 | Valore decimale rispetto ai byte | Potenze del 2 | Valore decimale rispetto ai byte |
| byte | B | 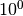 |
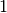 |
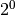 |
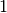 |
| kilobyte | kB | 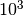 |
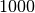 |
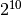 |
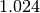 |
| megabyte | MB | 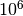 |
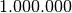 |
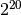 |
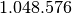 |
| gigabyte | GB | 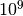 |
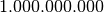 |
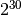 |
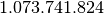 |
| terabyte | TB | 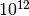 |
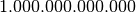 |
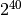 |
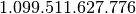 |
Osservazione
E’ noto che i prefissi kilo- Mega- e Giga- corrispondono a 1.000 , 1.000.000 (un milione) e 1.000.000.000 (un miliardo), mentre nell’informatica vengono impropriamente usati per indicare particolari potenze di 2.
Tutto questo genera confusione: per esempio un disco fisso che da specifiche
dovrebbe garantire una capacità di archiviazione pari a 160 gigabyte, quando ne
viene visualizzata la dimensione arriva poco oltre 149 gigabyte e i produttori
giocano su questa “incertezza”. I produttori fanno i conti
“imbrogliando”. Un PC che viene dichiarato con un hard disk da 160 GB
vengono trasformati in byte moltiplicando per 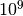 . Ma quando verifichiamo la grandezza del disco sull’elaboratore, il computer
divide per
. Ma quando verifichiamo la grandezza del disco sull’elaboratore, il computer
divide per 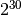 .
.
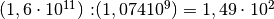 . Solo per questo “imbroglio” ci siamo persi 11 GB.
. Solo per questo “imbroglio” ci siamo persi 11 GB.
- Perché un DVD scrivibile quando si compra dichiara una capacità di 4,7 GB e invece ha una capacità reale di 4.3?Un CD-R dichiara una capacità di 700 MB. Quale è la sua capacità reale?.. tab[667,57 MB]
Operazioni in base diversa da dieci¶
Le quattro operazioni con i numeri in base diversa da dieci possono effettuarsi con gli stessi algoritmi utilizzati per i numeri naturali.
Esempio
| 0 | 1 | |
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Eseguire l’addizione in base 2 tra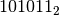 * e *
* e *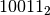
Dobbiamo tradurre in base due quello che facciamo in base dieci. Abbiamo perciò bisogno di costruire la tavola di addizione in base due che riportiamo a lato. La tavola, o tabellina, è piuttosto semplice, bisogna solo fare attenzione che in base due si ha 1+1=10, perché il 2 si scrive appunto 10 in base due.
| Riporti | **1 ** | **1 ** | |||||
| 1 | 0 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 0 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | 1 | 0 |
Mettiamo i numeri in colonna (vedi a fianco) e cominciamo ad addizionare a
partire dalle unità: 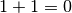 , scrivo
, scrivo 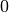
e riporto
.
- Nella colonna di ordine superiore trovo
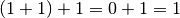
- Scrivo
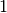 e riporto
e riporto 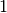
.
- Nella colonna di ordine superiore trovo
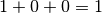
- scrivo
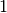 senza riportare alcunché.
senza riportare alcunché.
Continuo in questo modo fino ad esaurire tutte le cifre da addizionare.
Facciamo la verifica nell’usuale sistema decimale: 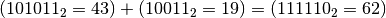
Esempio
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 10 |
| 2 | 2 | 3 | 4 | 10 | 11 |
| 3 | 3 | 4 | 10 | 11 | 12 |
| 4 | 4 | 10 | 11 | 12 | 13 |
Eseguire la somma tra **la somma **in base 5 tra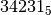 * e *
* e *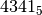
Costruiamo la tavola di addizione in base cinque: ricordiamo che 4+1=10, 4+2=11, ecc.
| **Riporti ** | 1 | 1 | 1 | |||
| 3 | 4 | 2 | 3 | 1 | ||
| 4 | 3 | 4 | 1 | |||
| 4 | 4 | 1 | 2 | 2 |
Mettiamo i numeri in colonna e cominciamo ad addizionare a partire dalle unità:
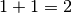
scrivosenza riporto.
Nella colonna di ordine superiore trovo 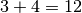 . Scrivo
. Scrivo 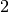
e riporto
.
- Nella colonna di ordine superiore trovo
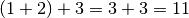
- scrivo
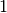 e riporto
e riporto 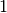
.
- Procedendo verso sinistra ora trovo
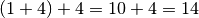
- scrivo
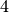 e riporto
e riporto 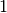
.
Infine 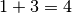 . L’addizione è terminata.
. L’addizione è terminata.
Verifica nel sistema decimale: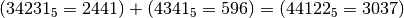
- Eseguire le seguenti addizioni in base 2
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |||||||||
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | ||||||||||||
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||||||||||||||||||||||||||
- Eseguire le seguenti addizioni in base 5
| 3 | 4 | 2 | 4 | 0 | 1 | 2 | 0 | 2 | 4 | 0 | 1 | 2 | 3 | 4 | 1 | 1 | 4 | 0 | 1 | 4 | 3 | 2 | 1 | ||||||||||
| 2 | 3 | 1 | 4 | 2 | 4 | 3 | 4 | 4 | 4 | 4 | 3 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | |||||||||||||||
| 3 | 4 | 4 | 3 | 4 | 0 | ||||||||||||||||||||||||||||
- Eseguire le seguenti addizioni in base 3
| 2 | 1 | 0 | 2 | 0 | 1 | 2 | 0 | 2 | 1 | 0 | 1 | 2 | 2 | 1 | 1 | 1 | 0 | 2 | 2 | 1 | 2 | 2 | 2 | ||||||||||
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 0 | 2 | 1 | 2 | 1 | ||||||||||||||
| 1 | 1 | 2 | 0 | 1 | 2 | 1 | 2 | ||||||||||||||||||||||||||
Per la sottrazione ci possiamo servire delle stesse tabelle dell’addizione.
Esempio
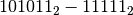
| **Riporti ** | -1 | -1 | -1 | ||||
| 1 | 0 | 1 | 0 | 1 | 1 |  |
|
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 1 | 1 | 0 | 0 |
Mettiamo i numeri in colonna e cominciamo a sottrarre partendo dalle unità:
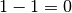
scrivo
.
- Nella colonna di ordine superiore trovo di nuovo:math:1 -1 =0
- scrivo
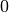
.
- Procedendo verso sinistra trovo
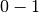
- devo quindi prendere in prestito un unità di ordine superiore che messa
- davanti a 0 diviene
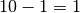
- scrivo
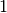 e riporto -
e riporto -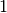
.
Mi sposto ancora a sinistra e trovo 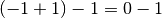 . Occorre prendere in prestito un’unità di ordine superiore
. Occorre prendere in prestito un’unità di ordine superiore 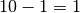 . Scrivo
. Scrivo 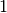
e riporto
.
- Nella colonna a sinistra ho
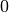
- del minuendo,
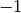 del riporto e
del riporto e 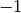 del sottraendo. Occorre prendere a prestito un’unità di ordine superiore
del sottraendo. Occorre prendere a prestito un’unità di ordine superiore - quindi
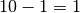
- a cui devo togliere
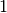 del sottraendo:
del sottraendo: 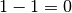
.
- Infine nella unità di ordine superiore devo addizionare il riporto
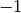
- a
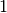 e scrivo ancora
e scrivo ancora 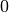
.Il risultato della sottrazione è: 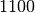
Verifica nel sistema decimale: 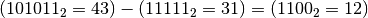
Esempio
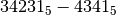 Ci serviamo della tavola di addizione in base cinque.
Ci serviamo della tavola di addizione in base cinque.
| 0 | 1 | 2 | 3 | 4 | |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 10 |
| 2 | 2 | 3 | 4 | 10 | 11 |
| 3 | 3 | 4 | 10 | 11 | 12 |
| 4 | 4 | 10 | 11 | 12 | 13 |
Verifica:.:math:( 34231_{5} =2441 )-( 4341_{5} =596 ) =( 24340_{5} =1845 )
- Eseguire le seguenti sottrazioni in base 2
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ||||||||||
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||||||||||
- Eseguire le seguenti sottrazioni in base 5
| 3 | 4 | 2 | 4 | 0 | 1 | 2 | 0 | 2 | 4 | 0 | 1 | 2 | 3 | 4 | 1 | 3 | 4 | 4 | 4 | 1 | 3 | 2 | 4 | 2 | |||||||||
| 2 | 3 | 1 | 4 | 2 | 4 | 3 | 4 | 4 | 4 | 4 | 3 | 1 | 2 | 3 | 4 | 2 | 2 | 4 | |||||||||||||||
- Eseguire le seguenti sottrazioni in base 3
| 2 | 1 | 0 | 2 | 0 | 1 | 2 | 0 | 2 | 1 | 0 | 1 | 2 | 2 | 1 | 1 | 1 | 2 | 0 | 1 | 2 | 1 | 0 | 0 | 1 | |||||||||
| 2 | 0 | 2 | 2 | 2 | 2 | 1 | 2 | 1 | 0 | 2 | |||||||||||||||||||||||
Adoperiamo lo stesso algoritmo usato per moltiplicare due numeri decimali utilizzando la tabella della moltiplicazione.
Esempio
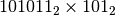
Dobbiamo tradurre in base due quello che facciamo in base dieci. Abbiamo perciò bisogno di costruire la tavola della moltiplicazione in base due.
| 1 | 0 | 1 | 0 | 1 | 1 | ´ | ||
| 1 | 0 | 1 | ||||||
| 1 | 0 | 1 | 0 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 0 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| ´ | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Verifica nel sistema decimale: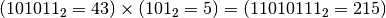
Esempio
| 2 | 3 | 1 | ´ | ||
| 2 | 4 | ||||
| 2 | 0 | 2 | 4 | ||
| 1 | 0 | 1 | 2 | ||
| 1 | 2 | 1 | 4 | 4 |
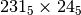
| ´ | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 11 | 13 |
| 3 | 0 | 3 | 11 | 14 | 22 |
| 4 | 0 | 4 | 13 | 22 | 31 |
Verifica nel sistema decimale 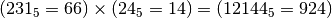
- Moltiplica in base 2:
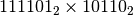 ;
; 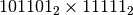 ;
; 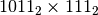
- Moltiplica in base 5:
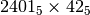 ;
; 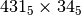 ;
; 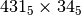
- Moltiplica in base 3:
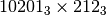 ;
; 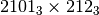 ;
; 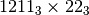
Anche per la divisione il procedimento è del tutto analogo a quello usato nel sistema decimale, la tavola da utilizzare è quella della moltiplicazione.
Esempio
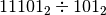
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
| -1 | 0 | 1 | 1 | 0 | 1 | |||
| 1 | 0 | 0 | ||||||
| 0 | 0 | 0 | ||||||
| 1 | 0 | 0 | 1 | |||||
| -1 | 0 | 1 | ||||||
| 1 | 0 | 0 |
Dobbiamo tradurre in base due quello che facciamo in base dieci.
- La cifra di ordine più alto si ottiene dalla divisione di
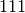
- con
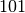
. Il quoziente è 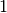 , il resto si ottiene dalla differenza tra il dividendo e il prodotto del
quoziente per il divisore. In questo caso il resto è
, il resto si ottiene dalla differenza tra il dividendo e il prodotto del
quoziente per il divisore. In questo caso il resto è 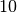 .
.
- Si abbassa lo
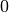
- e otteniamo
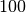
. Si ha 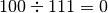 . La seconda cifra del divisore è
. La seconda cifra del divisore è 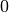 .
.
- La moltiplicazione di
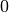
- per il divisore dà
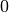
- . Il nuovo resto è
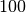
- a cui aggiungiamo l’ultima cifra del dividendo.
- Otteniamo
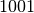
- che viene divisa
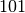
- . Il quoziente termina con
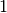
- con il resto uguale a
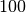
.
Verifica nel sistema decimale: 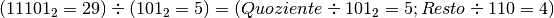
| 1 | 0 | 1 | ´ | ||
| 1 | 0 | 1 | |||
| 1 | 0 | 1 | |||
| 0 | 0 | 0 | ¾ | ||
| 1 | 0 | 1 | ¾ | ||
| 1 | 1 | 0 | 0 | 1 |
Eseguiamo la prova della divisione direttamente in base 2: 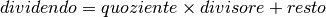
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 0 | |||
| 1 | 1 | 1 | 0 | 1 |
Il quoziente moltiplicato il divisore è uguale a 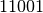 .
.
- Se a questo risultato aggiungiamo il resto
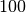
- otteniamo il dividendo
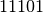
.
Esempio
Dobbiamo tradurre in base due quello che facciamo in base dieci.
| 3 | 4 | 0 | 2 | 4 | 2 | |
| 3 | 2 | 3 | 4 | 1 | ||
| 1 | 2 | 2 | ||||
| 4 | 2 | |||||
| 3 | 0 |
- Il
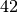
- nel
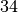 non ci sta. Prendiamo allora tre cifre
non ci sta. Prendiamo allora tre cifre 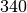
- . Il
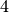
- nel
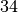 ci sta
ci sta 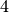 volte.:math:4
è la cifra di ordine più alto del quoziente. Dobbiamo trovare il resto. Il
volte.:math:4
è la cifra di ordine più alto del quoziente. Dobbiamo trovare il resto. Il - resto si ottiene sottraendo il risultato della moltiplicazione tra
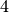
- e
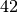
che è 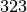 . Il resto è uguale
. Il resto è uguale 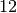 .
.
- Si abbassa il
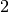
- e otteniamo
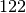
- . Il
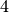
- nel
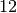 in base 5 ci sta una sola volta, infatti
in base 5 ci sta una sola volta, infatti 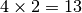
. La seconda cifra del divisore è 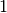 .
.
- La moltiplicazione di
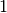
- per il divisore dà
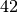
- . Sottraendo
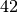
- da
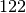 si ottiene
si ottiene 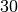
- . Dato che
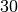
- è minore di
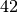 la divisione intera è terminata.
la divisione intera è terminata.
Verifica: 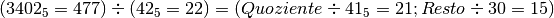
- Eseguire le seguenti divisioni in base 2
Copyright © Matematicamente.it 2011-12

Questo libro, eccetto dove diversamente specificato, è rilasciato nei termini della licenza Creative Commons Attribuzione – Condividi allo stesso modo 3.0 Italia (CC BY-SA 3.0) il cui testo integrale è disponibile al sito
http://creativecommons.org/licenses/by-sa/3.0/it/legalcode
Tu sei libero:
di riprodurre, distribuire, comunicare al pubblico, esporre in pubblico, rappresentare, eseguire e recitare quest’opera, di modificare quest’opera, alle seguenti condizioni:
Attribuzione — Devi attribuire la paternità dell’opera nei modi indicati dall’autore o da chi ti ha dato l’opera in licenza e in modo tale da non suggerire che essi avallino te o il modo in cui tu usi l’opera.
Condividi allo stesso modo — Se alteri o trasformi quest’opera, o se la usi per crearne un’altra, puoi distribuire l’opera risultante solo con una licenza identica o equivalente a questa.
Autori
Claudio Carboncini: teoria, esercizi
Anna Cristina Mocchetti: teoria, esercizi
Antonio Bernardo: coordinamento, esercizi
Germano Pettarin: esercizi
Angela D’Amato: integrazioni
Nicola Chiriano: correzioni
Francesco Daddi: esercizi
Erasmo Modica: teoria, esercizi
Mauro Paladini: integrazioni, esercizi
Vittorio Patriarca: integrazioni
Giuseppe Pipino: integrazioni, esercizi
Nicoletta Passera: esercizi
Daniele Zambelli: esercizi risultati
Luciano Sarra: correzioni
Nicola De Rosa: correzioni, risultati esercizi
Laura Todisco: correzioni
Gemma Fiorito: correzioni
Lucia Rapella: correzioni
Paolo Baggiani: correzioni
Simone Rea: osservazioni
Collaborazione, commenti e suggerimenti
Se vuoi contribuire anche tu alla stesura e aggiornamento del manuale Matematica C3 o se vuoi inviare dei commenti e/o suggerimenti scrivi a antoniobernardo@matematicamente.it
Versione del documento
Versione 3.1 del 24.04.2012
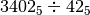
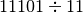
![[ Q = 11 ; R = 1 ]](_images/math/c61f3e8e76accd9047c96d9e028e55936776be9e.png)
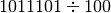
![[ Q = 1011 ; R = 1 ]](_images/math/2d395cf67ca769597f04d1bbbb03812d835198af.png)
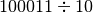
![[ Q = 10001 ; R = 0 ]](_images/math/b696487102ca9114e27ebcc816b99eff000be990.png)
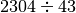
![[ Q = 24 ; R = 12 ]](_images/math/7d14b74e56737261c18f3d1deebe2229bb11d433.png)
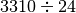
![[ Q = 112 ; R = 12 ]](_images/math/e4e0f85dd4cff12ea1fd96b747a07f2c70dbe5ed.png)
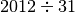
![[ Q = 31 ; R = 1 ]](_images/math/696db34a1ff89959bbf3332a887528ddc5338c57.png)